
【小6算数/文章題】幅のある特殊算は「値の範囲」がわかれば怖くない!|中学受験のツボ[算数編]
専門家・プロ
2023年1月18日
杉本啓太
0
保護者向けに中学受験の4教科のツボを解説。 算数編 は杉本啓太先生と有賀隆夫先生が担当します。
- 算数以外の3教科はこちら -
こんにちは、杉本です。
今回のテーマは、幅のある特殊算について。
特殊算の応用問題のなかには、基本的な解法を使っただけでは答えがひとつに決まらない問題が出てきます。たとえば「このような計算をしてでた数を四捨五入すると◯◯になりました」と問題文に書かれている場合、“四捨五入する前の値”をひとつに定めることができません。
こうした表現が問題に書かれていると混乱してしまう子は多いようですが、値がひとつに定まらないというのは、それほど難しいわけではありません。実は「値が定まらない」のではなく、「値に幅がある」と考えるだけで問題が簡単に解けることも多いのです。
そこで今回は「値に幅のある文章題」の解き方を、3つの例題を用いつつ紹介します。「難しいと思っていたけど、意外に解きやすい!」とお子さんが思うきっかけになればうれしいです。
Contents [hide]
- 四捨五入(切り上げ/切り捨て)をする問題
- 例題1
- 例題2
- “何人か”という表現のある「差集め算」
- まとめ
四捨五入(切り上げ/切り捨て)をする問題
四捨五入(切り上げ/切り捨て)をする問題について、ふたつの例題を解いてみましょう。
例題1
ひとつ目は、四捨五入のある問題です。
例題1:
ある整数Aに7をかけて1の位を四捨五入したところ、30になりました。もとの整数Aは何でしょう。
まず、この問題を式で書くとこうなります。
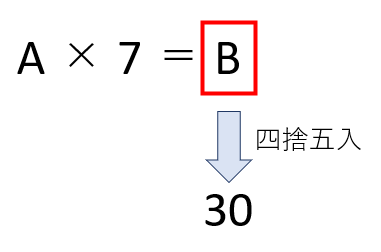
今回の問題のポイントは、四捨五入する前の値Bがはっきりとわからないこと。ただし四捨五入する前の値がわからなくても、値の範囲は求めることができます。
0
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

