
【小6算数/和と差の問題】人数の範囲を求める問題を線分図で解く|中学受験のツボ[算数編]
こんにちは。
株式会社ORA-Trio杉本です。
今回のテーマは「人数の範囲を求める問題」です。
特定の条件に当てはまる人として考えられる、最も多い人数・少ない人数を考える問題ですね。
このような問題は、ベン図を描いて取り組む子が多いかもしれません。
ただ、条件が複雑になってくると、ベン図だけだと状況を整理するのが難しい場合があります。
このようなとき、線分図を使った解法がおすすめです。
ベン図よりも視覚的に条件を表すことができるのです。そのため、お子さんによっては、線分図のほうが取り組みやすいという場合も多いですね。
今回は、例題を解きながら、「人数の範囲を出す問題」を解くときの線分図の描き方を解説します。
Contents [hide]
- 互いに独立な条件を含む問題の線分図の描き方
- 線分図による解法が有効な応用問題
- まとめ
互いに独立な条件を含む問題の線分図の描き方
まずは、基本的な図の描き方を紹介します。
次の例題を見てください。
例題1
40人のクラスで、「海が好きか、好きでない」「山が好きか、好きでない」のアンケートを取りました。その結果、海が好きな人は25人、山が好きな人は22人でした。海も山も好きな人は最も多くて何人、最も少なくて何人でしょう。
このような問題では、それぞれのアンケートの結果しか書いていません。「海を好きな人の◯割が山も好き」などの条件が書かれていないのです。
そのため、「海も山も好きな人」がちょうど何人か求めることはできません。
このような問題では、線分図を描いて考えてみるのがおすすめです。
例題1であれば、完成図は以下のようになります。
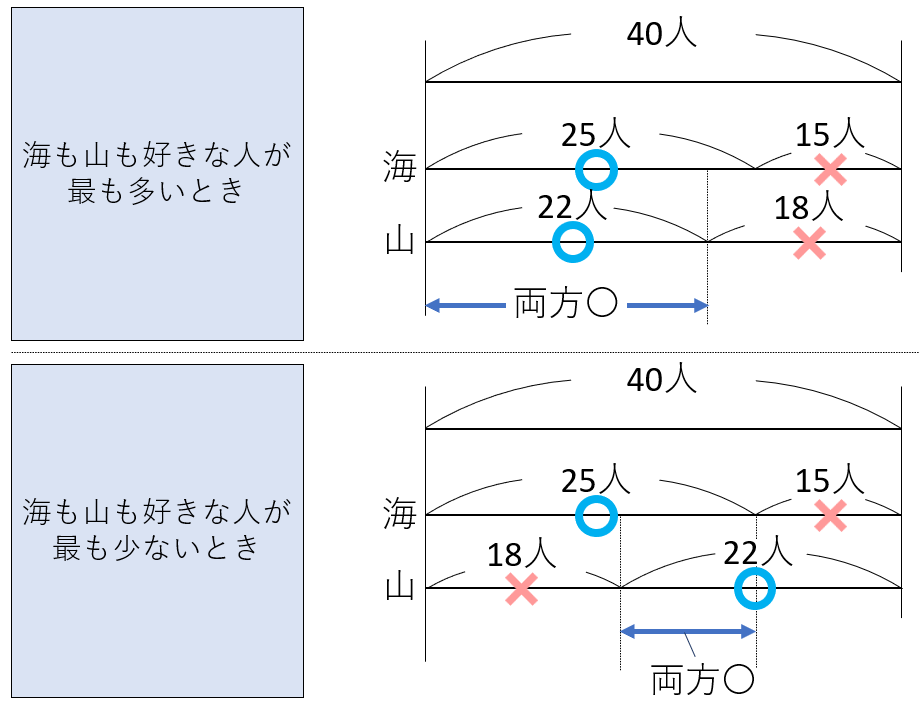
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

