
【小5算数/平面図形】半径のわからない円やおうぎ形の面積の求め方|中学受験のツボ[算数編]
こんにちは。
株式会社ORA-Trio杉本です。
今回のテーマは「半径のわからない円やおうぎ形の面積」です。
ある数を2回かけた数はわかるが、元の数は(小学校で習う範囲では)出せない、といった条件の問題ですね。
このような問題は、中学生以上であれば「平方根」といった考えを使えば解くことができます。「√(ルート)」の記号を使った数の表し方ですね。
でも「√」を使った表現は、中学受験では範囲外です。そのため、少し工夫が必要です。
今回は、このような数の問題を解くときの考え方とコツを解説します。
「半径のわからない円」の面積の求め方(式を使う方法)
まずは、「半径のわからない円の面積」の問題について、式を使った解法を解説します。
以下の例題を見てください。
例題1
下の図は、中心角90°のおうぎ形のなかに、1辺の長さが4cmの正方形を描いたものです。斜線部の面積は何㎠ですか。
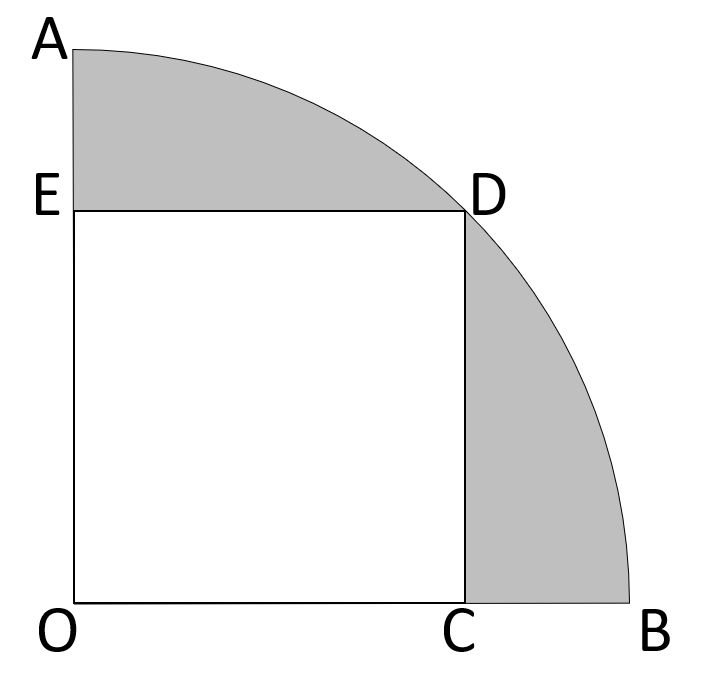
この問題を解くとき、お子さんはどのような方針で考えるでしょうか?
斜線部の面積を求めるために、「おうぎ形の面積から正方形の面積を引こう」と考える子は多いと思います。たしかに、正方形の面積は一辺の長さが4cmとわかっているので、求めることができますね。
問題は、おうぎ形の面積です。
おうぎ形の面積を出すには「円の半径×円の半径×3.14× \(\frac{1}{4}\) 」としたいですね。ところが、円の半径が問題文に書かれていないのです。
このようなときは、「円の半径と同じ長さが、どこかにないかな?」と考えてみましょう。
円の中心と円周上の点を結んだ長さは、すべて同じ長さです。すると今回は、OA、OBだけでなくODも円の半径であると気づくことができます。
また、ODは正方形の対角線の長さでもあります。
正方形の面積は、「対角線×対角線÷2」でも求めることができるのでした。
そのため、
対角線×対角線÷2=16から、
対角線×対角線=32
であることがわかります。
つまり、「円の半径×円の半径」も32ということですね。
今回、円の面積を「半径×半径×3.14× \(\frac{1}{4}\) 」で求めようとしていますね。ということは、半径はわからなくても、「半径×半径」がわかれば、面積を求めることができます。
解説は以下のとおりです。
1、正方形OCDEの面積は、4×4=16㎠
2、ODは正方形の対角線であるため、OD×OD÷2=16
したがって、OD×OD=32
3、ODは円の半径でもあるので、おうぎ形の面積「OD×OD×3.14× \(\frac{1}{4}\) 」で求めることができる
よっておうぎ形の面積は、
32×3.14× \(\frac{1}{4}\) =25.12㎠
4、斜線部の面積は、25.12-16=9.12㎠
まずは「半径がわからなくても、円やおうぎ形の面積を求めることができる場合がある」というイメージをしっかり持っておきましょう。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

