【小5算数／平面図形】内部底辺の考え方を使った三角形の面積｜中学受験のツボ［算数編］

国語｜理科｜社会

こんにちは。
株式会社ORA-Trio杉本です。

今回のテーマは「底辺も高さもわからない三角形の面積の求め方」です。

底辺・高さがわからない三角形を、2つの三角形に分割し、面積を求める方法について解説します。

今回紹介するのは、塾などでは「内部底辺」と呼ばれることもある方法です。平面図形の応用問題に取り組むときには、身につけておきたい考え方です。

「内部底辺の問題が解ける」だけでなく、特定の図形を見たときに「内部底辺の考え方を使ったら解ける問題だ」と反応できるよう、トレーニングしておけると良いですね。

今回は、まずは内部底辺の考え方と、それを使った面積の求め方について解説します。

その後、さらに同じ考え方を応用した問題にもチャレンジしてみましょう。

内部底辺の考え方

まずは、基本的な内部底辺の考え方と、それを使った面積の求め方について理解しましょう。

以下の例題を見てください。

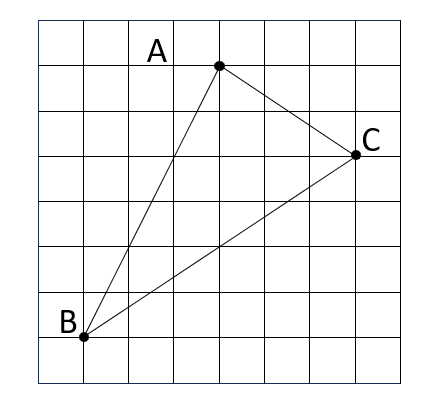
三角形ABCは、小学校の範囲では底辺や高さを求めることはできません。そのため「底辺×高さ÷2」以外の方法を考える必要があります。

たとえば、大きな正方形の面積から、まわりの三角形の面積をひき算するという方法があります。

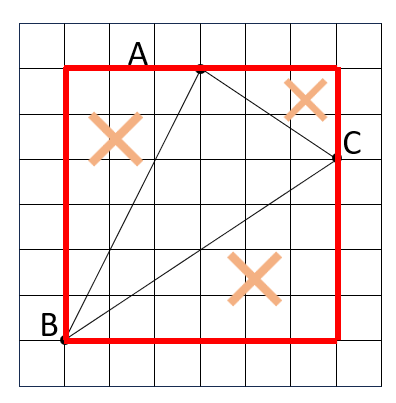
ただ、今回は「2つの三角形に分けて考える方法（内部底辺の考え方を使った方法）」を紹介したいと思います。

下の図のように、ABCを上下2つの三角形に分割するようにイメージしてみてください。

点Cから左に線を引き、辺ABと交わった点をDとします。そして、三角形ABCを三角形ADCと三角形BDCに分割します。

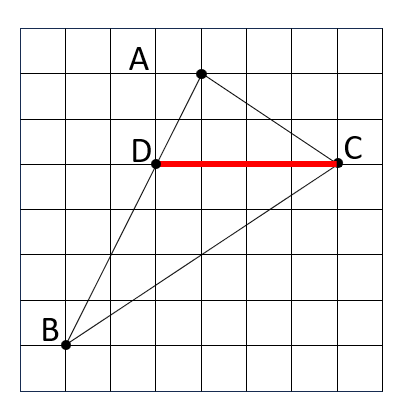
ここで、三角形ADCは、底辺がCDで高さが2cm、三角形BDCは、底辺がCDで高さが4cmの三角形です。

つまり、

三角形ADC＝CD×高さ（2cm）÷2
三角形BDC＝CD×高さ（4cm）÷2

と書くことができます。

よって、三角形ABCの面積は、以下のように求めることができます。

注意したいポイント

ここで注意してほしいポイントは、「三角形ADCの高さ＋三角形BDCの高さ」をまとめているところです。

この考え方を使えば、三角形ADCと三角形BDCそれぞれの高さがわからなくても、合計がわかれば面積が求まります。

このように、底辺や高さがわからなくても、内部の直線で三角形を2つに分け、それぞれの高さの和を使うことで面積を求められます。

この三角形を分割する直線（上図のCD）を「内部底辺」と呼ぶことがあります。

正式な名称というわけではありませんが、三角形を分割する考え方をうまく表現した呼び名だと思います。解法と合わせて覚えておけると良いでしょう。

「内部底辺」の考え方を使った応用問題

次に、内部底辺の考え方を使った応用問題にチャレンジしてみましょう。

以下の例題を見てください。

今回も、求める三角形を2つに分けて考えていきましょう。

三角形AGHは、辺EGによって、三角形HEGと三角形AEGに分けることができます。

三角形HEGと三角形AEGは、どちらも底辺はEGで11cm。

また、三角形HEGと三角形AEGの高さは合わせるとJDとなり、13－5＝8cm とわかります。

よって、解説は以下のようになります。

内部底辺の考え方はイメージできたでしょうか。

まとめ

今回は、底辺や高さがわからない三角形の面積を求めるときに使える「内部底辺」の考え方について解説しました。

平面図形は、理屈を理解しているだけでなく、演習による「慣れ」が重要な単元です。

図を見たときに「このやり方が使えるかもしれない」と気づけるようになるために、しっかりトレーニングを積んでおけると良いですね。

それではまた！

※記事の内容は執筆時点のものです