
【小4算数/分数】約分のコツと分子・分母の関係|中学受験のツボ[算数編]
髭之教育会代表の有賀です。
4年生の年間カリキュラム前半が終了しました。
個々の塾によって内容の前後はあります。ですが、受験算数の基礎となる内容については、おおむね学んだ子が多いと思います。
今回は、いままで学んだ内容だけで、入試問題に挑戦してみましょう。
「解法を単純作業として捉える」のではなく、「学んだ単元の本質を理解する」というのがポイントです。
これにより、4年生の知識でも十分に入試問題を解くことができます。
ぜひ挑戦してみてください!
Contents [hide]
- 約分は分母と分子の公約数探し
- 約分は分母と分子が互いに持っている数探し
- 「その数字が持っている数」の考え方で複雑な問題も解ける
約分は分母と分子の公約数探し
約分のやり方を教えるときに、
「分母と分子両方を割れる数を探してごらん。見つけたら、分母も分子もその数で割ってね」
と説明されることが多いと思います。
もちろん、約分をする方法を端的に表したわかりやすい説明です。
では、ここでもう一歩踏み込んで、約分について考えてみましょう。
決して数学的に掘り下げて、難しい話をするわけではありません。4年生でもわかる、あたりまえのことについて説明します。
確認してほしいことは次の2点です。
- 約分は分母と分子の「公約数を探している」
- 公約数とはそれぞれの整数の因数である
「1」の公約数の意味は覚えている子が多いでしょう。
忘れていても、「共通の約数だよね」というヒントで思い出すことがほとんどです。
次に、2の「因数」という言葉がくせ者かもしれません。
たとえば「24の因数は?」と聞かれたら、
24=2×2×2×3
素因数分解(かけ算の形に分解)したそれぞれの数のことです。
この場合なら2、2、2、3が24の因数ですね。
素因数分解のやり方は、約数・倍数の単元で学んだ「すだれ算」を数字ひとつでやるだけです。
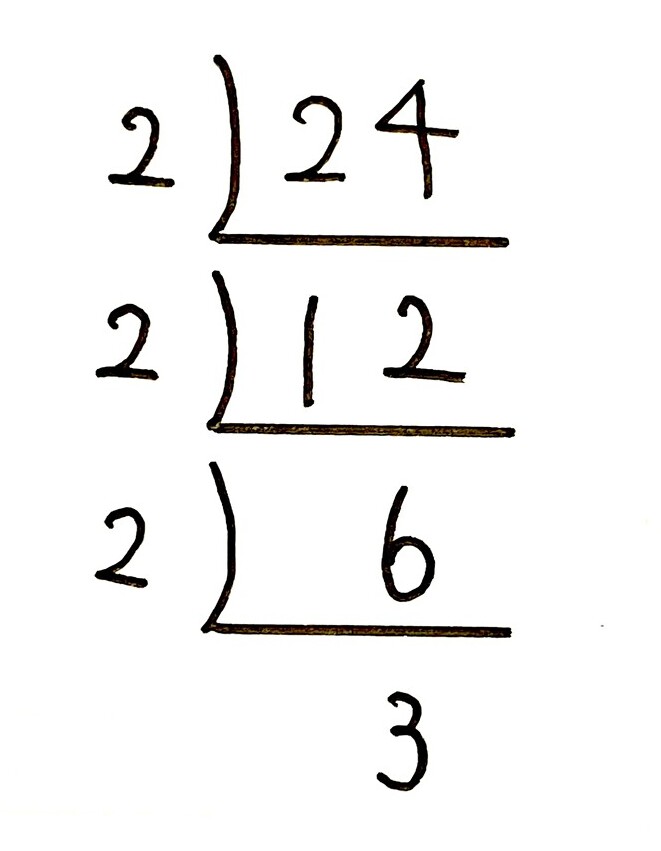
僕は算数があまり得意ではない子には、因数という言葉は使いません。「その数が持っている数」という言い方にしています。
非常に大ざっぱな表現ですが、算数嫌いの子にはイメージしやすいようです。ぜひ試してみてください。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

