
【小6算数/平面図形】方眼を使った図形の面積の求め方|中学受験のツボ[算数編]
こんにちは。
株式会社ORA-Trio杉本です。
今回のテーマは「方眼を使った問題」です。
方眼とは、規則正しく真四角にくぎったマス目のことです。たて・よこの線が引かれた紙のことを「方眼紙」といいますが、あの「方眼」ですね。
この「方眼」に描かれた図形の問題を解くときは、ふだんとは少し違う解法を使うときがあります。中学校で「座標」や「作図」の単元で習う内容ですが、中学受験で出題されることも珍しくありません。
今回は、まず方眼に描かれた三角形の面積の求め方を紹介したあと、それを利用した応用問題について解説します。
Contents [hide]
- 方眼を使った三角形の面積の求め方
- 方眼を使った応用問題
- まとめ
方眼を使った三角形の面積の求め方
まずは、方眼を使った三角形の面積の求め方です。
以下の例題を見てください。
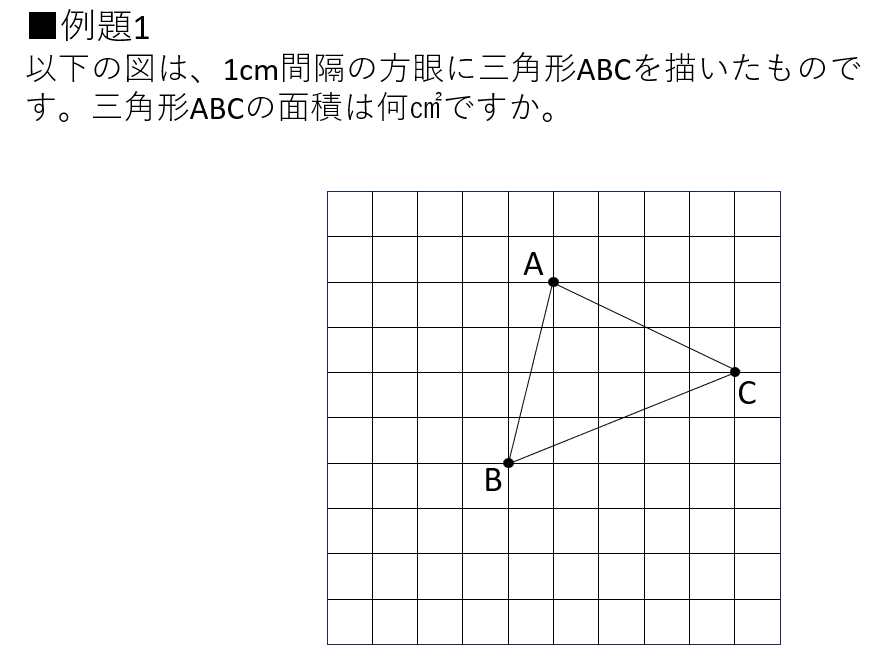
三角形の面積は、「底辺の長さ×高さ÷2」という公式で求める子が多いと思います。
でも今回の問題では、どこを底辺としても、「底辺の長さ」を求めるのは少し難しそうです。
このようなときに有効なのが「周りを長方形で囲んで、不要な部分の面積を引く」という解法です。
方眼をなぞって、求める三角形を囲むような長方形を描いてみましょう。すると、下のような図になります。
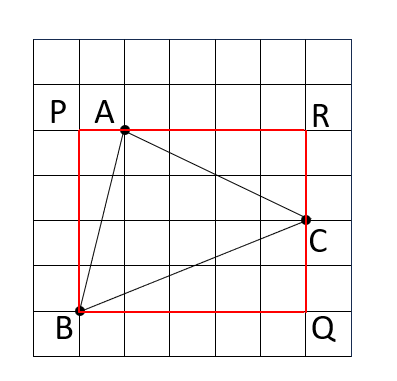
ここで、長方形PBQRは2辺の長さがわかるので、面積を求めることができます。
また、求める三角形以外の部分、つまり三角形PBA、三角形BQC、三角形CRAは、すべて直角三角形となっています。
こちらも、直角をはさむ2辺の長さがわかるので、面積を求めることができます。
そして、三角形ABCの面積は、長方形PBQRから三角形PBA、三角形BQC、三角形CRAの面積を引くことで求めることができます。
解法は以下のとおりです。
1、長方形PBQRの面積は4×5=20㎠
2、三角形PBAの面積は、4×1÷2=2㎠
3、三角形BQCの面積は、5×2÷2=5㎠
4、三角形CRAの面積は、2×4÷2=4㎠
5、三角形ABCの面積は、20-2-5-4=9㎠
一つひとつの計算はそこまで難しくありませんね。ただ、出てくる図形は多くなります。
見まちがいをしないよう、式を丁寧に書いていきましょう。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

