
【小6理科/物理】音の速さの計算問題 ―― 2種類の問題に対応できるようにしよう|中学受験のツボ[理科編]
こんにちは、倉石です。
「音の速さの計算問題」が苦手な受験生は多いかもしれません。
しかし、計算の際に用いる解法は、算数の「速さ」の基本問題で出てくるものばかりです。
今回はふたつのパターンに分けて、音の速さの計算問題の解き方を説明します。
Contents [hide]
- 音の速さの計算問題
- 1、音源や観測者が動かない問題
- 2、音源や観測者が動く問題
- まとめ
音の速さの計算問題
音の速さは「温度」によって異なります。
0℃のときは、秒速約331.5mです。そこから温度が1℃高くなるごとに、秒速は約0.6m早くなります。
この数字を正確に覚える必要はありませんが、「15℃のときの音速は秒速約340m」ということは覚えておくと便利です。
では実際に、音の速さを用いた問題を考えていきましょう。
音の速さの問題は、大きく分けて2種類あります。
- 音源や観測者が動く問題
- 音源や観測者が動かない問題
1、音源や観測者が動かない問題
まずは「動かない場合」から考えていきましょう。
【例題1】
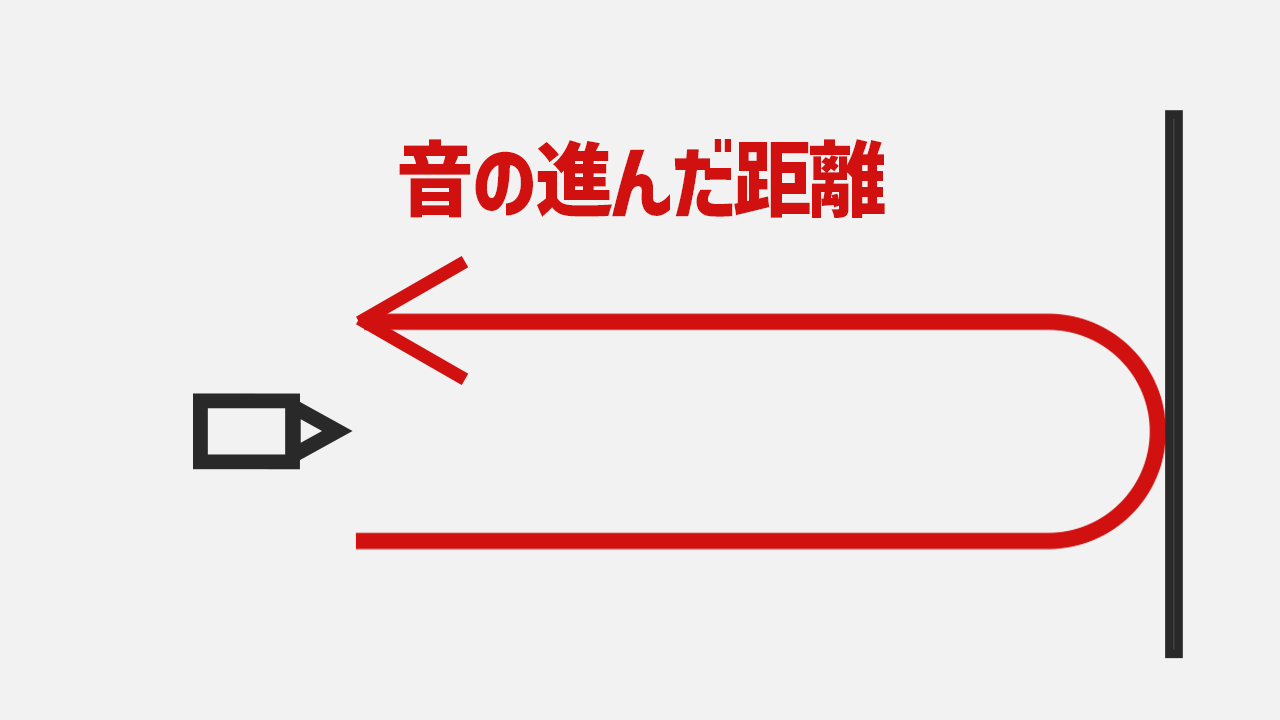
岸壁からある距離にいる船が汽笛を鳴らし始めると、5秒後に音が聞こえ始めました。
船は、岸壁から何mのところにいるでしょうか? ただし、音速は毎秒340mとします。
このパターンの問題は、算数で扱う「速さ」の基本的な問題として考えることができます。
速さが毎秒340m、時間が5秒なので、
音が動いた距離は 340×5=1700m です。
しかし、これは答えではありません。
今回の問題では、船から出された音は岸壁で反射し、また船に返ってきます。そのため音が動いた距離は、船から岸壁までの距離の2倍になります。
よって岸壁までの距離は、1700÷2=850m です。
このように音源も観測者も動かない場合は、速さの問題として解くことができます。
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

