
倍数と約数の教え方(2)公倍数と公約数は小さな数のかけ算の形にしてみる|ママのための受験算数の教え方プチ講座
「倍数」「約数」のうち2つ以上の整数において「公倍数」「公約数」というものが存在します。さらにそこには、「最小公倍数」「最大公約数」も存在します。その定義は、次のようになります。
公倍数:いくつかの整数に共通な倍数
最小公倍数:公倍数のなかで、一番小さな数
公約数:いくつかの整数に共通な約数
最大公約数:公約数のなかで、一番大きな数
今回は公倍数と公約数のあらゆる問題に対応できるような、ちょっとしたテクニックをお伝えします。
Contents
公倍数/公約数の見つけ方
ここでも「倍数と約数の教え方(1)」に述べたように、数をかけ算の形で表すことが重要です。さらに、公倍数と公約数の問題を解くには小さな数のかけ算の形で表す(素因数分解)ことがポイントになります。
「12」と「30」の公倍数/公約数
例として、「12」と「30」の公倍数と公約数を考えてみましょう。
まずは「12」をかけ算の形に表します。
12=2×6
この「6」はさらに、「6=2×3」と表すことができますよね。したがって、
12=2×6=2×2×3
といった具合にかけ算で表すことができます。整数の範囲では、これ以上は小さな数のかけ算に表すことができませんね。数をこれより小さなかけ算にできない状態まで分解することを素因数分解といいます。素数に分解するという意味です。
同様に「30」を小さな数のかけ算に表すと、
30=2×15=2×3×5
と表すことができます。
「12」と「30」の公約数と最大公約数を見つける
あとは、この2つのかけ算を並べて見比べるとわかってきます。
12と30、この2つの数に共通するものは、
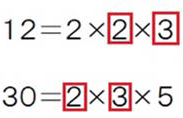
2、3ですよね。したがって、共通する約数、つまり公約数は、
1、2、3、6(=2×3)
です。
そしてこのなかで一番数の大きいもの、つまり最大公約数は6となります。
「12」と「30」の公倍数と最小公倍数を見つける
「12」の倍数というのは、「12×○」の形で表せる数です。つまり、

の形で表されます。
同様に「30」の倍数は「30×△」の形で表せるものですから、

の形で表されます。
よって、「12」と「30」の共通の倍数(「12」の倍数であり、かつ「30」の倍数である数)つまり「12」と「30」の公倍数は、

の形で表すことができ、
「12」と「30」の公倍数は「60」の倍数であるといえる。そして最小公倍数は「60」である。
と導くことができます。
まずは、上のような例で小さな数のかけ算にする作業(素因数分解)によって、公倍数と公約数の仕組みをお子さんにしっかりと理解させてみてください。
公倍数・公約数の標準的問題
それでは、次の問題を考えてみましょう。
■問題(標準)
8でわっても12でわっても5あまる2けたの整数のうち、最小のものを求めよ。
まずは、お子さんに「問題文を文通りに式にしてごらん」と誘導して解かせてください。
文のままですよ!!
文のままを式にするとは、

というふうにするということです。この2つの式を言い換えると、

となります。そして、言い換えた2つの式を並べて見比べさせてください。すると何かに気づいてくれると思います。
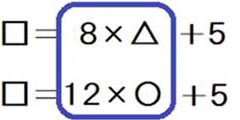
青枠の箇所が「8の倍数であり、12の倍数である」つまり、「8と12の公倍数である」ことに気づけばよいです。
青枠の箇所を、小さな数のかけ算の形に表しましょう。
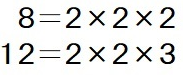
これにより、「8」と「12」の公倍数は、
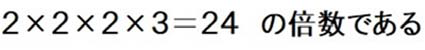
よって、求める数は
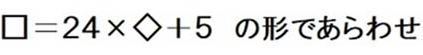
その2けたの数の最小値は、
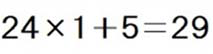
答えは「29」となります。
または、次のように解いていってもいいです。
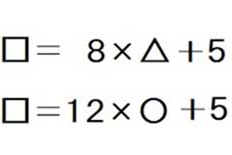
この段階で小さな数のかけ算で表すと
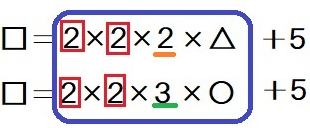
これより、
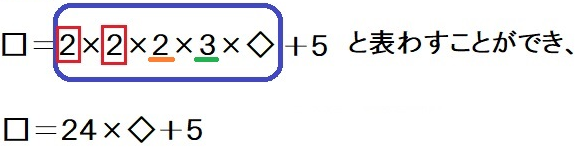
これを満たす2けたの最小値は、
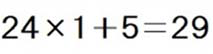
答えは「29」となります。
この問題は最小公倍数の問題ですが、それには途中の式を書きながら気づけばよいことです。それ以上にお子さんには小さな数のかけ算(素因数分解)の形にしてみることで解決につながることを知ってもらいたいです。
まとめ ――小さな数のかけ算の形にしてみる
倍数・約数はかけ算の形で表すことを基本にしながら、さらに小さな数のかけ算の形にまで変形(素因数分解)することで、応用的な問題にも対応できるようになります。
特に公倍数と公約数は、上記の例で紹介したような、小さな数のかけ算に現れた数で構成されている数になります。
かけ算の形に表したら、もうひと工夫。小さな数のかけ算の形で表すテクニックも身につけさせてみてください。
■ママのための受験算数の教え方プチ講座 バックナンバー
- 数と式の処理の教え方(3)☐を使った式
- 数と式の処理の教え方(2)計算のきまりと工夫
- 数と式の処理の教え方(1)計算の順序
- 割合の教え方(3)百分率、歩合のステップアップ
- 割合の教え方(2)百分率、歩合の定義通りの解法
- 割合の教え方(1)割合の定義、百分率、歩合
- 倍数と約数の教え方(5)倍数、公倍数の実践問題
- 倍数と約数の教え方(4)約数の個数
- 倍数と約数の教え方(3)かけ算の形から、倍数・約数に気づく
- 倍数と約数の教え方(2)公倍数と公約数は小さな数のかけ算の形にしてみる
- 倍数と約数の教え方(1)かけ算の形に表す
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

