
倍数と約数の教え方(5)倍数、公倍数の実践問題|ママのための受験算数の教え方プチ講座
倍数と約数の教え方(1)、(2)において、倍数と公倍数についての基本的な考え方を紹介しました。今回はそれらをベースとした実践問題にチャレンジしてもらい、どのように基本事項が使われ、さらにどんな力が要求されるのかを知ってもらいたいと思います。
倍数、公倍数の実践問題
さっそく次の実践問題をお子さんに解いてもらいましょう。
■問題(難)
3を引くと4の倍数になり、2をたすと7の倍数となるような整数について、次の問に答よ。
(1)このような整数のうち、2けたの数をすべて求めよ。
(2)このような整数のうち、3けたの数は何個あるか。
どうでしょうか、お子さんは無事答えを出すことができましたか?
まずは問題文「2をたすと7の倍数になり、3を引くと4の倍数となるような整数」の通りに式をつくってみます。
求める整数を☐とすると、
☐-3=4×○、 ☐+2=7×△ (○、△:整数)
この式をそれぞれ変形すると、
☐=4×○+3、 ☐=7×△-2
となり、ここまでは大丈夫だと思います。
この先この2式を同時に満たす整数□を見つけ出すのには、少し実践力が必要になると思いますが、間違いなく「倍数と約数の教え方(1)、(2)」の内容で解ける問題です。
では、倍数、公倍数の基本事項をお子さんに再確認させながら、実践力を養うために、次の2つの問題(問題1、問題2)を解きながら、力つけていきましょう。まずは問題1からです。
■問題1(基礎)
4の倍数でも7の倍数でもある2けたの整数をすべて求めよ。
解説
この問題は4の倍数(4×○の形)であり、7の倍数(7×△の形)でもある整数である、つまり7と4の公倍数の問題です。
7と4の公倍数とは、最小公倍数28の倍数(28×□の形)です。
そのうち2けたの整数は
28×1=28、 28×2=56、 28×3=84より
答えは28、56、84である。
ここで倍数と公倍数についての仕組みを考えてみましょう。仕組みを考えるために、それぞれの倍数を書き並べて、見比べてみます。
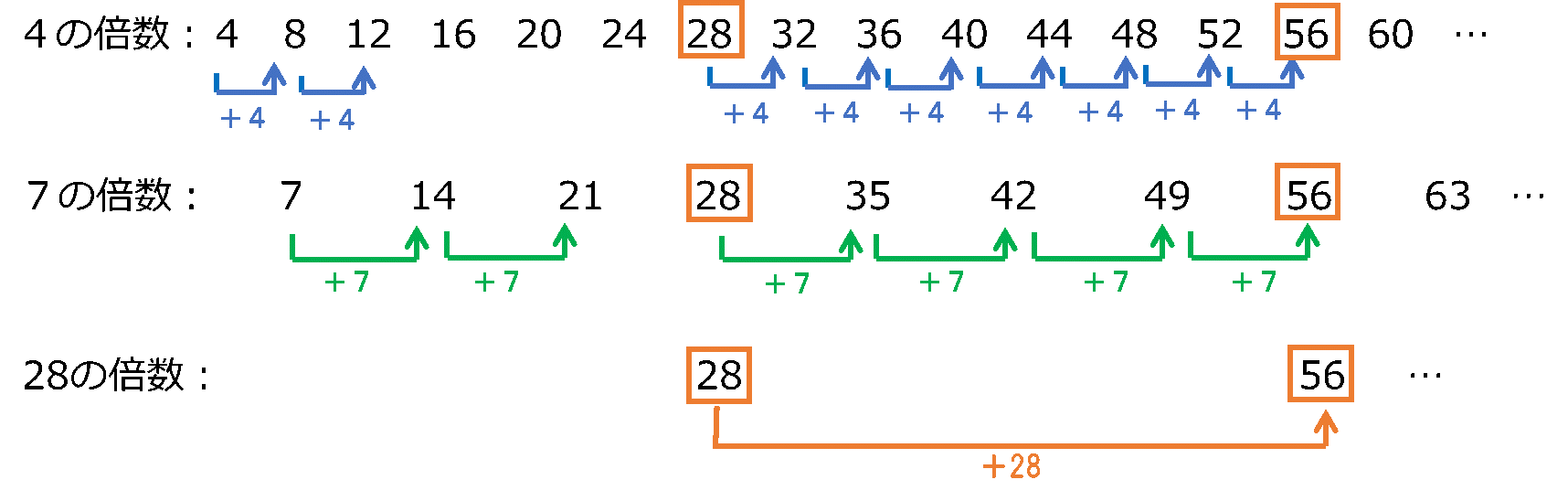
4の倍数は4ずつ増え、7の倍数は7ずつ増えので、「4の倍数でも7の倍数でもある数」は4と7の最小公倍数28ずつ増える。つまり28の倍数であることが目で確認できます。
次に問題2です。
■問題2(標準)
50から100までの整数のうち、2をたすと7の倍数となる整数の個数を求めよ。
(ここまででつまずいてしまう場合は「倍数と約数の教え方(1)」の倍数の個数を求める問題の解き方を確認しましょう)
解説
まず、求める整数(2をたすと7の倍数となる整数)を☐とします。
☐+2=7×△ (△は整数)
☐=7×△-2
そして、ここからが実践力を要します。何をするのかというと、具体的に書き出すのです。(簡単でしょ!)この具体的に書き出してみる方法は、意外と受験算数に強くなる方法なのです。
さっそく、
54、61、68、…、96
また、これを「7×△-2の形」で表すことによって、仕組みが理解できます。

また、△は順番を表していることがわかります。そして求める数は8番目から14番目の数である。
さらに「7×△-2」を1番目から書き出してみると、さらに理解しやすくなります。

1番目から7番目までがいらないので、
答えは14-7=7(個)である。
では、再度本題を解いてみましょう。
■問題(難)
3を引くと4の倍数になり、2をたすと7の倍数となるような整数について、次の問に答よ。
(1)このような整数のうち、2けたの数をすべて求めよ。
(2)このような整数のうち、3けたの数は何個あるか。
解説
求める整数を☐とすると、2つの条件は、
☐-3=4×○、 ☐+2=7×△ (○、△:整数)
と表せます。この2式をそれぞれ変形すると、
☐=4×○+3、 ☐=7×△-2
これらを具体的に書き出し、書き並べ、見比べると、
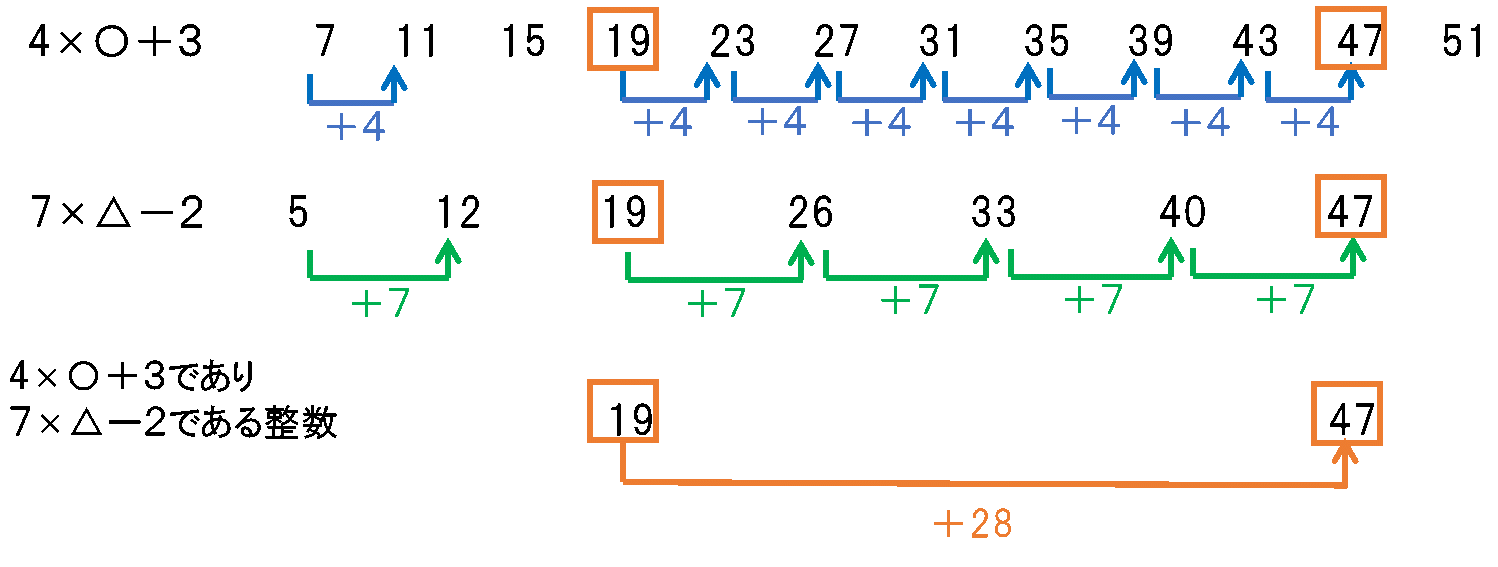
よって、求める整数□は次々に28を加えたものであることがわかります。
つまり、求める整数は
□=28×△+19 (△は整数)
と表すことができます。
■問(1)
2けたの整数を具体的に書き出すと、
19、 19+28=47、 47+28=75 よって、
答えは19、47、75である。
■問(2)
3けたの整数は
103、131、…999
であり、これを「28×△+19の形」で表すと、

である。
これは、2番目までがいらないと考えられるので、
3けたの整数の個数は
35-2=33個
答えは33個である。
まとめ ――具体的に書き出す、書き並べる、見比べる
算数(数学)の実践力を養うには、基本事項をしっかりと身に付けたうえでまずは、
- 具体的に書き出す
- 書き並べる
- 見比べる
をやるといいです。簡単なことなのですが、意外とこの3つのことを試さずに「格好の良い式」ばかり探す子は多いです。
- 具体的に書き出して、その数の仕組みに慣れる
- きれいに書き並べて、その規則性(構造)を考える
- 見比べて、その構造を深く理解する
ことが大切です。
最後に理解した構造を、式で表現していくことは、力のいる作業だと思います。
今回の場合、「求める整数□は次々に28を加えたものであることがわかる。求める整数は□=28×△+19(△は整数)と表すことができる」という部分が、最後の式での表現にあたります。
でも、基本的な行動は「具体的に書き出す、書き並べる、見比べる」ととても簡単なものなので、お子さんが問題に悩んでいる場合は、「具体的に書いてみたら?」「きれいに並べて書いてみたらどう?」「書き並べたものを見比べて見てごらん」と声をかけてあげるだけでも、実践力を養えると思います。そして、この「具体的に書き出す、書き並べる、見比べる」は整数を求める問題にとても有効です。
■ママのための受験算数の教え方プチ講座 バックナンバー
- 数と式の処理の教え方(3)☐を使った式
- 数と式の処理の教え方(2)計算のきまりと工夫
- 数と式の処理の教え方(1)計算の順序
- 割合の教え方(3)百分率、歩合のステップアップ
- 割合の教え方(2)百分率、歩合の定義通りの解法
- 割合の教え方(1)割合の定義、百分率、歩合
- 倍数と約数の教え方(5)倍数、公倍数の実践問題
- 倍数と約数の教え方(4)約数の個数
- 倍数と約数の教え方(3)かけ算の形から、倍数・約数に気づく
- 倍数と約数の教え方(2)公倍数と公約数は小さな数のかけ算の形にしてみる
- 倍数と約数の教え方(1)かけ算の形に表す
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

