
割合の教え方(3)百分率、歩合のステップアップ|ママのための受験算数の教え方プチ講座
割合の教え方(1)(2)での「定義通りの立式による解法」を十分に理解できたなら、次は「簡素な式」を使うとより解答しやすくなります。今回はこの簡素な式に慣れながら、ややレベルの高い問題にチャレンジしてみましょう。
簡素な式を身に付ける
■練習問題
(1)みかん250個の72%は何個でしょうか。
(2)お父さんの体重はみのるさん体重の1.75倍で、お父さんの体重は63kgです。みのるさんの体重は何kgでしょうか。
(3)ある品物を2割引きで買うと720円です。この品物の定価はいくらでしょうか。
解説
(1) [簡素な式を使った解法]
72%=\frac{72}{100}=0.72より
250×\frac{72}{100}=180 …①
または250×0.72=180
よって、180個
これらの式は定義通りの解法の途中式です。実際に(1)を定義通りの解法で解くと次のようになります。
(1)[定義通りの解法]
求めるみかんの個数を☐個とすると
もとにする量…250個
比べられる量…☐個
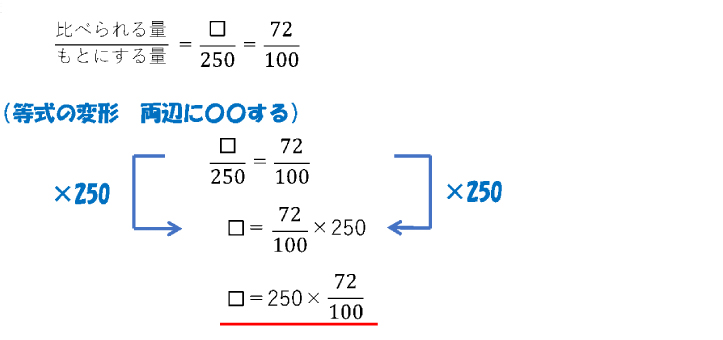
赤線部分に①の式が出てくる。
(2)[簡素な式を使った解法]
みのるさんの体重を☐kgとすると、
☐×1.75=63 …②
より
☐=63÷1.75=36
よって、みのるさんは36kg
(2)を定義通りの解法で解くと次のようになります。
(2)[定義通りの解法]
みのるさんの体重を☐kgとすると
もとにする量…みのるさんの体重☐kg
比べられる量…お父さんの体重63kg
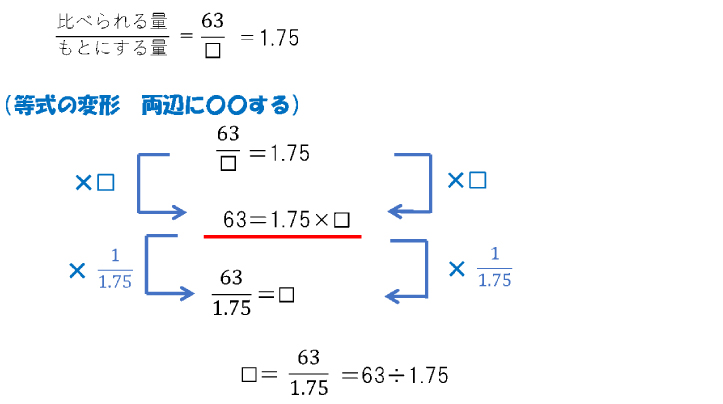
赤線部分に②の式が出てくる。
(3)[簡素な式を使った解法]
品物の定価を☐円とする
2割引きとは、10割-2割=8割のことである。また8割=\frac{8}{10}=0.8である。
☐×\frac{8}{10}=720 …③
この等式の変形の基本である両辺への変形を行い
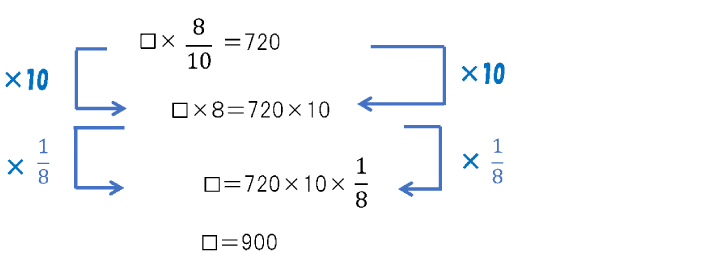
または、
☐×0.8=720より
☐=720÷0.8=900
よって定価は900円
(3)を定義通りの解法で解くと次のようになります。
(3)[定義通りの解法]
もとにする量…定価 ☐円、 比べられる量…720円より
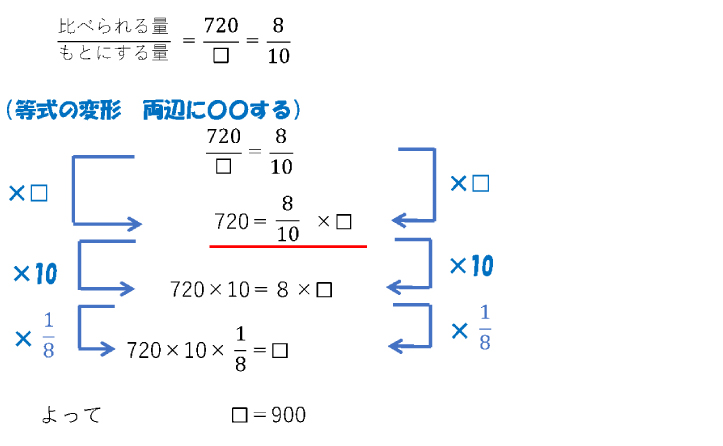
赤線部分に③の式が出てくる。
お子さんが、割合の問題に十分に慣れ、理解できているなら①②③式のような簡素な式も使うとよいでしょう。ただし、立式に悩んでる場合は、「定義通りの解法」に戻って理解し直してください。
ややレベルの高い問題にチャレンジ
基本や標準問題に慣れてきたら、ステップアップしてみましょう。次の問題をお子さんにチャレンジさせてみてください。
■問題(やや難)
ある映画館の当日の入場者に対する女性の割合は、昨日は54%、今日は60%でした。今日は昨日より、入場者全体が15%減り、女性の入場者は18人減りました。昨日の入場者は何人だったでしょう。
解説
求めたい昨日の入場者の人数をA人とします。
昨日の女性の入場者は、昨日の入場者全体の54%より、
A×\frac{54}{100} (人)
今日の入場者数は昨日の入場者の15%少ないことより、100-15=85%であるから、
A×\frac{85}{100} (人)
さらに今日の女性の入場者数は、今日の入場者全体の60%より
(A×\frac{85}{100})×\frac{60}{100} (人)
今日は昨日の女性の入場者は18少ないことより、
A×\frac{54}{100}-(A×\frac{85}{100})×\frac{60}{100}=18
と立式できます。あとはこれを解けばよいです。
この式を処理していくときにも、等式の変形(両辺に〇〇する)を繰り返していきます。
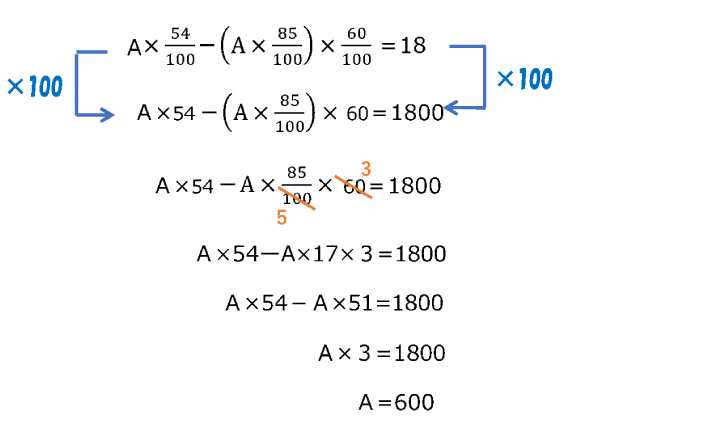
よって、昨日の入場者は600人である
まとめ ――「定義通りの解法」を理解したら、「簡素な式」を使う
割合の「定義通りの立式による解法」が十分にできるようになったなら、次は「簡素な式」を使う練習をすると良いでしょう。この簡素な式は、解答をシンプルすることができ、とても便利です。この「簡素な式」は「定義通りの解法」の途中の式にあたるので別の考えのものではありません。やさしい問題で「定義通りの解法」を十分に理解したあと、「簡素な式」で表す訓練をし、徐々に問題のレベルアップをしてみてください。しかし、お子さんが問題の理解に困ってきたら、再び定義に戻り解き直してみると解消できると思います。
■ママのための受験算数の教え方プチ講座 バックナンバー
- 数と式の処理の教え方(3)☐を使った式
- 数と式の処理の教え方(2)計算のきまりと工夫
- 数と式の処理の教え方(1)計算の順序
- 割合の教え方(3)百分率、歩合のステップアップ
- 割合の教え方(2)百分率、歩合の定義通りの解法
- 割合の教え方(1)割合の定義、百分率、歩合
- 倍数と約数の教え方(5)倍数、公倍数の実践問題
- 倍数と約数の教え方(4)約数の個数
- 倍数と約数の教え方(3)かけ算の形から、倍数・約数に気づく
- 倍数と約数の教え方(2)公倍数と公約数は小さな数のかけ算の形にしてみる
- 倍数と約数の教え方(1)かけ算の形に表す
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

