
倍数と約数の教え方(4)約数の個数|ママのための受験算数の教え方プチ講座
倍数と約数の教え方(1)、(2)、(3)において、「倍数、約数、公倍数、公約数」とかけ算の関係、さらに小さな数のかけ算(素因数分解)の便利さについて少しおわかりいただけたと思います。
では、徐々に実践問題に入っていましょう。
約数の個数を求める問題
まずは、小さな数の約数の個数を求める問題をお子さんに解いてもらいましょう。
■例(小さな数の約数の個数)
54の約数の個数を求めよ。
答えは8個です。お子さんの答えはあってましたか? では、確かめてみましょう。
54の約数とは、54を割り切ることができる整数です。
例えば、
54÷6=9
なので、6は54の約数となります。
かけ算の形「54=6×9」に表すこともできます。
54の約数を小さい方から書き出すと、
1、2、3、6、9、18、27、54
よって8個です。
お子さんは過不足なく8個の約数を出すことはできましたか?
(もちろん具体的に約数を出す方法とは別の解法もあります。その場合は途中の考え方や途中式はきちんと表されていますか?)
では次に、大きな数の約数の個数を求めてみましょう。
■重要問題(大きな数の約数の個数)
540の約数の個数を求めよ。
まずは、お子さんに自由に解かせてみてください。
答えは24個です。
解説
こういった大きな数の場合は、約数を思いつくまま書き出していると、過不足が生じやすくなります。ですので、過不足なく数える工夫が重要なポイントです。
これまでのおさらいですが、倍数・約数はかけ算の形に表すと考えやすくなります。さらに、小さな数のかけ算の形(素因数分解)に表すことで約数の構造を知ることができます。
ですから、まずは540を小さな数のかけ算の形で表してみましょう。次のような形まで小さなかけ算の形に表せればOKです。
540=2×2×3×3×3×5
さらに、540の約数は
540=□×〇
と表せる整数□、〇であるといえます。
例えば、

または、

といった具合です。
つまり、540の約数は2、2、3、3、3、5のかけ算で作られているのです。これが約数の構造といえます。
この構造を念頭に、約数を規則正しく、過不足なく書き出していきます。
540の約数をかけ算の個数の順に書くと、

※過不足なく数えることが重要です
よって24個となります。
この問題は約数の作られ方=約数の構造を理解し、それを使って約数を過不足なく見つけ出すことがポイントです。
上記の場合、過不足なく約数を見つけ出すには、まずかけ算の個数で分類しながら、かけ算の中の小さい数の順番、つまり2×□、その次に3×□と規則を設けて書き出すことが大切です。
規則の設け方は、お子さんの工夫に任せてもよいですが、規則を設けて、相手にも伝わるように書き出すことが、約数の構造を理解するうえでも重要です。
また、入試では学校によりますが、途中式を書いて解答する場合もあります。その場合は、次のような解答ができるとよいでしょう。
■解答例
540=2×2×3×3×3×5 より
540の約数は2、2、3、3、3、5のかけ算で表される。
約数を書き出すと、
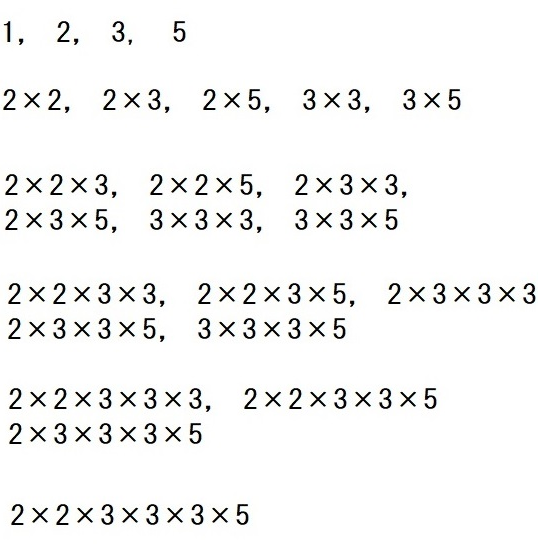
よって、540の約数の個数は24個
ちなみに、この「540の約数の個数」は高校数学の教科書にも出てくる問題です。高校では540の約数は2が2個、3が3個、5が1個の積で表されるので、
(1+2)×(1+3)×(1+1)=3×4×2=24個
と解いていきます。
お持ちの参考書等でも、
この(1+2)×(1+3)×(1+1)の式を紹介しているものもあると思いますが、お子さんが、式の意味を理解できていない状態で、丸暗記で解くのは、あまりおすすめしません。
なぜなら、もし何らかの応用が加わった場合、そのまま使えないことがあるからです。それよりは、お子さんが理解できる方法で解答力をつけていく方が、本番の入試に強い子ができます。
では、もう一問。次はやや難しい問題です。
■問題(やや難)
3けたの整数で、約数が3個だけの整数のうち最小のものを求めよ。
ここでも、約数の構造が大切ですよ!
解説
まず、約数が3個だけの整数の約数のひとつは 1 です。
ということは、1以外の約数が2つしかないということになります。また、その2つのうち、ひとつは「その整数自身」です。
具体的には△=□×〇と表されたとき□と〇は△の約数であり、さらに△の約数は必ず1と△の2つを持ちます。
ここで△の約数が3個だけであるということは、その約数は、

であるといえますよね。
また、□と〇が異なる場合、△=□×〇の約数は最低でも、

の4個が存在することになりますが、この問題は「約数が3個」なのですから、

とすればよい。つまり、
△=□×□の形のみで表されます。
よって、約数が3個だけの整数は、□×□の形で表すことができ、□は素数(それ以上割り切ることができない数)である。
そのうち、3けたになる整数は
11×11、 13×13、 17×17、…
であり、最小のものは11×11=121である。
まとめ ――約数の構造(約数の作られ方)を理解して、過不足なく書き出す
今回の要点は「約数の構造(約数の作られ方)を理解すること」と「過不足なく数える(書き出す)こと」でした。これを意識した解答を心がけるといいと思います。
ここで再度注意しますが、受験用の問題に数多く取り組む中で、複雑で意味の分からない公式を知ることがあると思います。ですが、公式の丸暗記に頼るような勉強の仕方は決してさせないでください。中学受験の後には中学数学、高校数学(大学受験数学)と続きます、「暗記中心の勉強」は特に、高校数学において潰れてしまう原因になりかねません。
算数を学ぶうえで、意識してほしいのは「内容の理解」。今回は約数の構造(約数の作られ方)の理解です。
実際に、問題2のような問題では、公式は通用せず約数の構造の理解が必要です。今は中学受験のためですが、せっかくのお子さんの勉強ですし、将来に役立つような勉強の仕方に導いてあげてください。
■ママのための受験算数の教え方プチ講座 バックナンバー
- 数と式の処理の教え方(3)☐を使った式
- 数と式の処理の教え方(2)計算のきまりと工夫
- 数と式の処理の教え方(1)計算の順序
- 割合の教え方(3)百分率、歩合のステップアップ
- 割合の教え方(2)百分率、歩合の定義通りの解法
- 割合の教え方(1)割合の定義、百分率、歩合
- 倍数と約数の教え方(5)倍数、公倍数の実践問題
- 倍数と約数の教え方(4)約数の個数
- 倍数と約数の教え方(3)かけ算の形から、倍数・約数に気づく
- 倍数と約数の教え方(2)公倍数と公約数は小さな数のかけ算の形にしてみる
- 倍数と約数の教え方(1)かけ算の形に表す
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

