
倍数と約数の教え方(3)かけ算の形から、倍数・約数に気づく|ママのための受験算数の教え方プチ講座
倍数と約数の教え方(1)、(2)で、「倍数と約数はかけ算の形に表す」「公倍数と公約数については、さらに小さな数のかけ算の形(素因数分解)に表す」ことをお伝えしました。今回は、途中式に出てきたかけ算の形から倍数・約数に気づくことによって解決していく問題を取り扱ってみます。
Contents [hide]
途中式でのかけ算の形への対応問題
■問題(標準)
クッキーが32個、チョコレートが45個あります。何人かの子どもに、同じ数ずつクッキーとチョコレートを分けたら、クッキーは2個、チョコレートは3個残ります。子どもは全部で何人いましたか。ただし、子どもは2人以上います。
まずは、文章題の基本「問題文通りに式をつくってごらん」とお子さんに声をかけてください。もちろん、求めたいものやわからないものは〇、△、▢を使ってください。(文字が使えるお子さんにはx,y、zを使わせてもいいです)
次のような2つの式をつくります。

受験を意識するなら、何を▢に置いたのかを記す癖は必要です。そして、この状態で〇、△、▢は整数だとわかります。
なぜなら、
〇:1人につきのチョコレートの数ですから整数です。
△:1人につきのクッキーの数ですから整数です。
□:子どもの人数だから整数です。
この2つの式をそれぞれ変形すると、
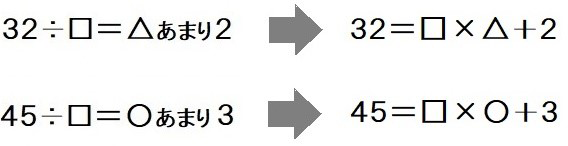
となります。
これを整理して、次の式にします。

さらに式を変形させます。
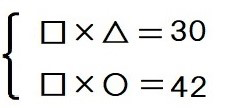
この状態でお子さんに「このかけ算の式から、何か言えないかな?」と訊ねてみてください。
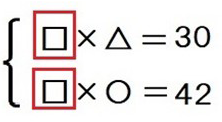
この2つのかけ算の式から倍数、約数であることに気づくとよいです。
「30と42はともに□の倍数である」または、「□は30と42の公約数である」といえます。
これを小さなかけ算(素因数分解)の形で表すと、
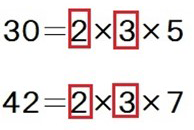
となります。したがって、30と42で共通する約数つまり公約数は、
1、2、3、6(=2×3)
ということがわかります。
ここで注意しなければならないのが、問題文に
クッキーは2個、チョコレートは3個残ります
とあるので子どもの人数は3より多いとわかります。
求める子どもの人数は6人となります。
また、次のように解いてもいいです。
小さなかけ算(素因数分解)の形で表しながら解きます。
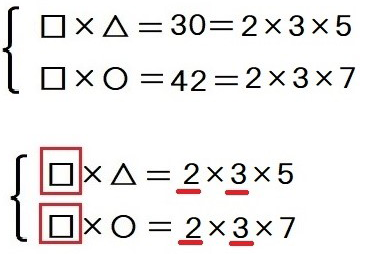
これより、□にあてはまる数は、
1、2、3、6(=2×3)
である。
問題文に
クッキーは2個、チョコレートは3個残ります
とあるから、求める子どもの人数は6人である。
この問題は最大公約数の問題ですが、問題文のなかにはどこにも記載されていません。問題文を立式し、その式の変形の途中で出てきたかけ算の形から、求める数が約数であることに気づき、解答する必要があります。
またこのとき、かけ算の形をさらに小さな数のかけ算(素因数分解)の形にすると、約数であるという意識を持たずとも処理することもできます。
まとめ ――途中で現れる式を上手く整理・変形する
問題を解く途中で現れる式を上手く整理・変形することで、解決の糸口が見つかります。今回は途中で現れるかけ算の式から倍数、約数に気づくことで解決できるのですが、「気づく」という行動はやはり、倍数・約数・公倍数・公約数の本質(構造)がしっかりと理解できていないと気づけません。
受験算数の応用問題に対応するためには、土台となるその本質(構造)を身につける必要があります。この倍数・約数の本質を理解するには「倍数と約数(2)」での例が適当であると思います。このやさしい例を今一度お子さんに理解させながら、しっかりと土台を築いてあげてください。
また、小さな数のかけ算(素因数分解)の形はとても役立つ形です、問題を解く途中で行き詰ったりしたときは、この小さな数のかけ算の形へ変形をしてみると何かを気づかせてくれるかもしれません。
■ママのための受験算数の教え方プチ講座 バックナンバー
- 数と式の処理の教え方(3)☐を使った式
- 数と式の処理の教え方(2)計算のきまりと工夫
- 数と式の処理の教え方(1)計算の順序
- 割合の教え方(3)百分率、歩合のステップアップ
- 割合の教え方(2)百分率、歩合の定義通りの解法
- 割合の教え方(1)割合の定義、百分率、歩合
- 倍数と約数の教え方(5)倍数、公倍数の実践問題
- 倍数と約数の教え方(4)約数の個数
- 倍数と約数の教え方(3)かけ算の形から、倍数・約数に気づく
- 倍数と約数の教え方(2)公倍数と公約数は小さな数のかけ算の形にしてみる
- 倍数と約数の教え方(1)かけ算の形に表す
※記事の内容は執筆時点のものです
とじる
お気に入り機能は
会員の方のみご利用できます
会員登録のうえログインすると
お気に入り保存できるようになります。
お気に入りのコンテンツは、
マイページから確認できます

