数と式の処理の教え方（2）計算のきまりと工夫｜ママのための受験算数の教え方プチ講座

「数と式の処理の教え方（1）」の計算の順序で正しい答えにたどり着くことはできるようになったと思います。今回は、計算のきまりについてお伝えします。計算のきまりを知ったうえで、工夫して計算ができればより楽に式を処理し、計算力を強化していくことができます。

特に問題文に「くふうして計算」と書かれている場合は、「工夫の仕方」も採点対象になります。つまり途中の式が採点対象ですので、採点者に工夫の様子がわかるように途中式を書く訓練をするとよいです。後述する、重要問題の3つは、中学受験に向けた算数だけでなく、その後の数学（高校数学、大学受験数学）にも役立つ内容なので、ぜひ身につけていただきたいです。

計算のきまり［1］数を入れ換えて計算してもよい ――交換法則

計算のなかには、数を入れ換えて計算してもよいものがあり、これを「交換法則」といいます。次のように、たし算とかけ算は数を入れ換えて計算できますが、ひき算とわり算は入れ換えができません。

このように、交換法則が成り立つ（数を入れ換えて計算できる）のは、たし算とかけ算だけです。お子さんに説明するときには、「△＋☐＝☐＋△」ではなく、次のように簡単な数字を使った式で説明すると、理解しやすくなります。

それでは、次の例で計算の工夫にチャレンジしてみましょう。

たし算とかけ算は数を入れ換えて計算できる（交換法則が成り立つ）ので、上手く入れ換えて計算しやすくしましょう。

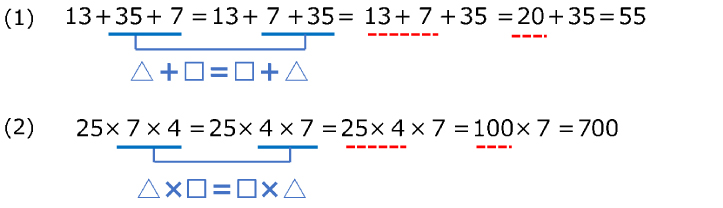
この（1）（2）の例から、交換法則の成り立つ（数を入れ換えて計算できる）たし算とかけ算には、次の性質が成り立つことがわかります。

これを実際に簡単な数字を使った式で表すと、次のようになります。

しかし、ひき算とわり算ではこの性質は成り立ちません。

計算のきまり［2］それぞれに分配して計算 ――分配法則

カッコをつかった計算にも、きまりがあります。「分配法則」と呼ばれるもので、それぞれに分配して計算するものです。次の形に表すことができます。

この計算（それぞれに分配する計算）を矢印で記すと、次のようになります。

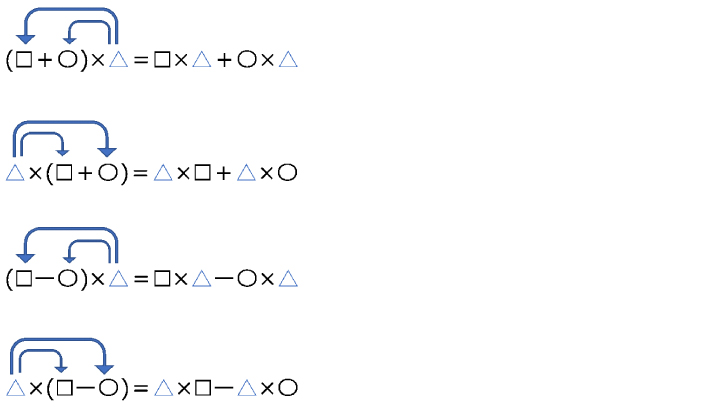
さらに、実際に簡単な数字を使った式で表すと、次のようになります。

計算のきまり［3］――くくりだす

分配法則「△×(☐＋〇)＝△×☐＋△×〇」を「△×☐＋△×〇＝△×(☐＋〇)」と書き直すと。左の式の中には「△×　」が共通に存在しています。右の式では、その△をまとめた形になっています。このことを「共通なものでくくる」といいます。（これは、数学で習う因数分解で最も大事な行動です!!） この「共通なものでくくる」で一番はじめに習うものが、小学2年生の「ー（マイナス）」でのくくりだしです。このマイナスでのくくりだしは、次の形に表すことができます。

実際に簡単な数字を使った式で表すと、次のようになります。

計算のきまりを使った、実践問題

では、これまでに紹介した計算のきまりを使った、実践問題をやってみましょう。

どのように工夫したかが重要なので、途中式は必ず書かせてください。

まず、それぞれの式は今回紹介した計算のきまりのなかのどれを使うとよいでしょうか？ それを知るには、式や数の特徴を見つけるといいです。

解説

（1）　38×13＋38×17

共通な数字「38」に注目すると、「△×(☐＋〇)＝△×☐＋△×〇」が使えます。この式を書き変えると「△×☐＋△×〇＝△×(☐＋〇)」ですから、（1）の式と見比べると「△は38である」ことがわかってきます。

分配法則の式を逆に書いた「△×☐＋△×〇＝△×(☐＋〇)」この式の変形の仕方は「共通なものでくくる」といわれるものです。これは数学の因数分解をするときに、1番目に取り組む式変形で、とても重要なものです。ぜひお子さんに身につけさせてあげてください。

（2）　48×25

ここでは「25」の便利な使い方を知ってもらいたいです。それは「25×4＝100」であること。25は「4」があれば便利に使えるので、ここでは次のようにわざわざ「4」を出してみます

使った計算のきまりは「△×☐×〇＝(△×☐)×〇＝△×(☐×〇)」です。

（3）　76×99

ここでは「99」の「見方を変える」ことがポイントです。その見方とは、「99＝100－1」でもありますね。

「2けた×2けた」の計算が「7600－76」という簡単なひき算で求められます。

使った計算のきまりは「△×(☐－〇)＝△×☐－△×〇」です。

また、この「99＝100－1」という見方は高校数学（大学受験数学）でも使う処理の仕方でもあります。この機会にお子さんにしっかりと身につけてあげておくと、その後の大学入試でも役立ちます。

まとめ ――計算のきまりを知って、工夫する

算数（数学）で求められる力は「工夫する力」と「表現する力」です。ただ単に式のはじめから頑張って計算して、その計算スピードを上げていくのではなく、工夫することで楽に計算をしていくことが重要です。そして、その工夫を表現するためには、暗算ではなく途中式を書くことは不可欠です。

お子さまの勉強を、近くで見守っているサポーターのお母さまが「何か工夫できないかな？」「その工夫を式で書いてみよう」と声かけてあげるだけで、徐々にお子さんの解答は良くなっていくと思います。（計算のクセは、一番近くにいる方の指導が効果あります）

また、今回の重要問題の3つは、計算の工夫の代表的なものです。この機会に工夫の仕方を知り、類似の問題での練習をするといいと思います。

■ママのための受験算数の教え方プチ講座 バックナンバー

• 数と式の処理の教え方（3）☐を使った式
• 数と式の処理の教え方（2）計算のきまりと工夫
• 数と式の処理の教え方（1）計算の順序
• 割合の教え方（3）百分率、歩合のステップアップ
• 割合の教え方（2）百分率、歩合の定義通りの解法
• 割合の教え方（1）割合の定義、百分率、歩合
• 倍数と約数の教え方（5）倍数、公倍数の実践問題
• 倍数と約数の教え方（4）約数の個数
• 倍数と約数の教え方（3）かけ算の形から、倍数・約数に気づく
• 倍数と約数の教え方（2）公倍数と公約数は小さな数のかけ算の形にしてみる
• 倍数と約数の教え方（1）かけ算の形に表す

※記事の内容は執筆時点のものです