倍数と約数の教え方（1）かけ算の形に表す｜ママのための受験算数の教え方プチ講座

中学受験を念頭に算数の学習をしていくうえで欠かせないのが「倍数」「約数」の理解です。

「ある整数を整数倍してできる数」を、もとの整数の「倍数」といい、「ある整数をわりきることができる整数」をもとの整数の「約数」といいます。

こういった定義も含め、倍数や約数の性質・関係を深く理解するためには、その表現方法を知っておくと効果的です。

倍数・約数はかけ算の形で表す

倍数・約数の問題を解くうえでのポイントは、お子さんに途中式をかけ算の形で表わさせることです。

たとえば、

「12は3の倍数である」 ⇒ 12＝3×4

と表すと、文にはない4という数字が自然とでてきますね。

そして、実はこの4には大きな意味があるのです。

12＝3×4

これは「12は3の倍数の4番目」であるともいえます。このことを使って、ちょっとした問題が解けるようになるのです。

（もちろん「12＝3×4」から、「3は12の約数である」という言い換えもできることは、お気づきですよね）

一定の区間内で、ある数の倍数の個数を求める問題

正答は「249個」ですが、お子さんの解いた途中式をよく見てください。次のように回答していないでしょうか。

この回答・書き方は間違いではありませんが、今回のポイント「倍数をかけ算の形に表すこと」を意識させて、お子さんに「かけ算の形に表してごらん」と声をかけながら、

999＝4×249＋3

もしくは

996＝4×249

という式を導いてあげてください。

そして、お子さんに「249はどういう意味？」と訊ねながら、「4の倍数の249番目」を理解させてみてください。次のような回答ができるようになれば、まずはOKです。

続いて、次のような形の問題を考えてみましょう。

正答は「225個」ですが、次の例のような間違いが多くみられます。

「249－25＝224」というところで、その前の計算で出てきた数をなんとなく引いてしまうと間違いになります。

こうしたミスの原因は、計算によって出てくる「249」「25」という数の意味を理解していないところにあります。

お子さんにきちんとかけ算の形で書かせ、それが4の倍数の何番目であるかを表していることを理解させながら、この問題の内容を目で見える形にします。

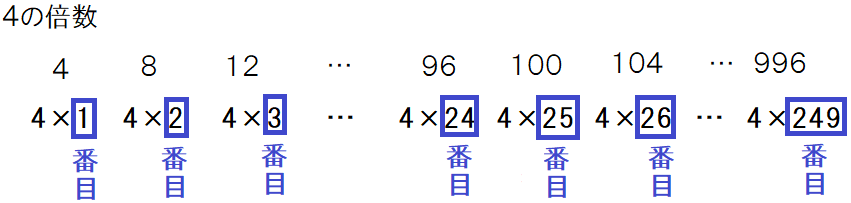
さらに、求めたい「3けたの整数」の箇所を確認すると、

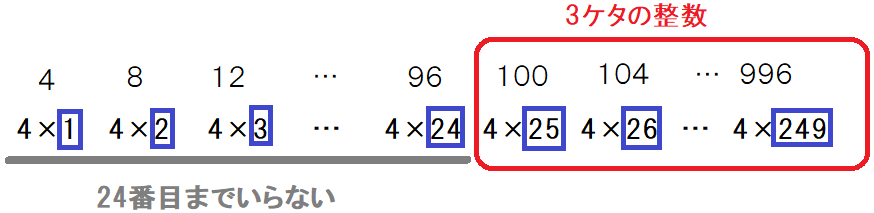
25番目～249番目までが求める「3けたの整数」です。そして、上の図からこのことを言い換えると「24番目までがいらない」ということになります。これによって次の式が自然にできあがります。

この例題は、1つずれた誤答を誘うよくある引っ掛け問題です。この種の問題で誤答を防ぐには、意味のある式をつくり、目で確認しながら考えるような表現のしかたを知るとよいと思います。

まとめ ――倍数・約数はかけ算の形で表しながら解く

倍数・約数はかけ算の形で表しながら解くと、倍数・約数の本質が見えてきます。これによって、難問に対応できる力も育成されます。ぜひ、お子さんの途中式の書き方も丁寧にサポートしてあげてください。

倍数や約数に関する問題は、将来高校で学ぶ数学（数列）でも良く扱われるので、途中式の書き方や何番目の理解を身に付けておくと役に立つと思います。

■ママのための受験算数の教え方プチ講座 バックナンバー

• 数と式の処理の教え方（3）☐を使った式
• 数と式の処理の教え方（2）計算のきまりと工夫
• 数と式の処理の教え方（1）計算の順序
• 割合の教え方（3）百分率、歩合のステップアップ
• 割合の教え方（2）百分率、歩合の定義通りの解法
• 割合の教え方（1）割合の定義、百分率、歩合
• 倍数と約数の教え方（5）倍数、公倍数の実践問題
• 倍数と約数の教え方（4）約数の個数
• 倍数と約数の教え方（3）かけ算の形から、倍数・約数に気づく
• 倍数と約数の教え方（2）公倍数と公約数は小さな数のかけ算の形にしてみる
• 倍数と約数の教え方（1）かけ算の形に表す

※記事の内容は執筆時点のものです